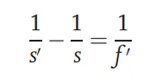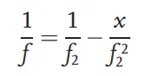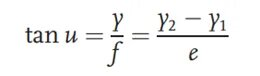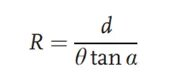1. Optisten järjestelmien polttoväli
Polttoväli on erittäin tärkeä optisen järjestelmän indikaattori. Polttovälin käsitteestä meillä on enemmän tai vähemmän ymmärrystä, jota tarkastelemme tässä.
Optisen järjestelmän polttoväli, joka määritellään etäisyydeksi optisen järjestelmän optisesta keskipisteestä säteen polttopisteeseen, kun valo osuu säteeseen yhdensuuntaisesti, mittaa valon keskittymistä tai hajaannusta optisessa järjestelmässä. Käytämme seuraavaa kaaviota havainnollistamaan tätä käsitettä.
Yllä olevassa kuvassa vasemmasta päästä tuleva yhdensuuntainen säde, kuljettuaan optisen järjestelmän läpi, suppenee kuvan polttoväliin F'. Suppenevan säteen käänteinen jatkoviiva leikkaa tulevan yhdensuuntaisen säteen vastaavan jatkoviivan pisteessä. Tämän pisteen ohittavaa ja optiseen akseliin nähden kohtisuoraa pintaa kutsutaan takapäätasoksi. Takapäätaso leikkaa optisen akselin pisteessä P2, jota kutsutaan pääpisteeksi (tai optiseksi keskipisteeksi). Pääpisteen ja kuvan polttovälin välistä etäisyyttä kutsutaan yleensä polttoväliksi. Koko nimi on kuvan efektiivinen polttoväli.
Kuvasta voidaan myös nähdä, että etäisyyttä optisen järjestelmän viimeisestä pinnasta kuvan polttopisteeseen F' kutsutaan takapolttoväliksi (BFL). Vastaavasti, jos yhdensuuntainen säde tulee oikealta puolelta, on olemassa myös käsitteet efektiivinen polttoväli ja etupolttoväli (FFL).
2. Polttovälin testausmenetelmät
Käytännössä on monia menetelmiä, joilla voidaan testata optisten järjestelmien polttoväliä. Eri periaatteiden perusteella polttovälin testausmenetelmät voidaan jakaa kolmeen luokkaan. Ensimmäinen luokka perustuu kuvatason sijaintiin, toinen luokka käyttää suurennuksen ja polttovälin välistä suhdetta polttovälin arvon saamiseksi ja kolmas luokka käyttää konvergoituvan valonsäteen aaltorintaman kaarevuutta polttovälin arvon saamiseksi.
Tässä osiossa esittelemme yleisesti käytettyjä menetelmiä optisten järjestelmien polttovälin testaamiseen::
2.1Collimaattorimenetelmä
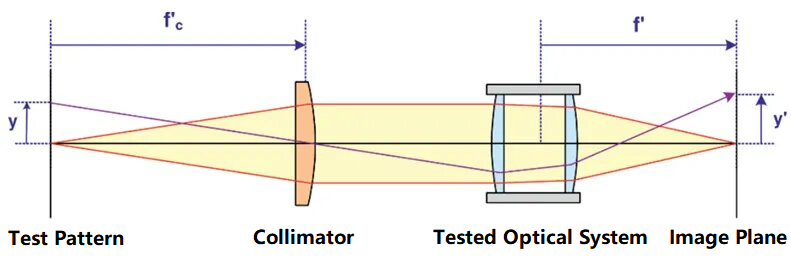
Kollimaattorin käytön periaate optisen järjestelmän polttovälin testaamisessa on esitetty alla olevassa kaaviossa:
Kuvassa testikuvio on sijoitettu kollimaattorin polttopisteeseen. Testikuvion korkeus y ja polttoväli fcKollimaattorin polttovälit y' tunnetaan. Kun testattava optinen järjestelmä on konvergoinut kollimaattorin lähettämän yhdensuuntaisen säteen ja kuvannut sen kuvatasossa, optisen järjestelmän polttoväli voidaan laskea kuvatasossa olevan testikuvion korkeuden y' perusteella. Testattavan optisen järjestelmän polttoväli voidaan laskea seuraavalla kaavalla:
2.2 Gaussin jakaumaMmenetelmä
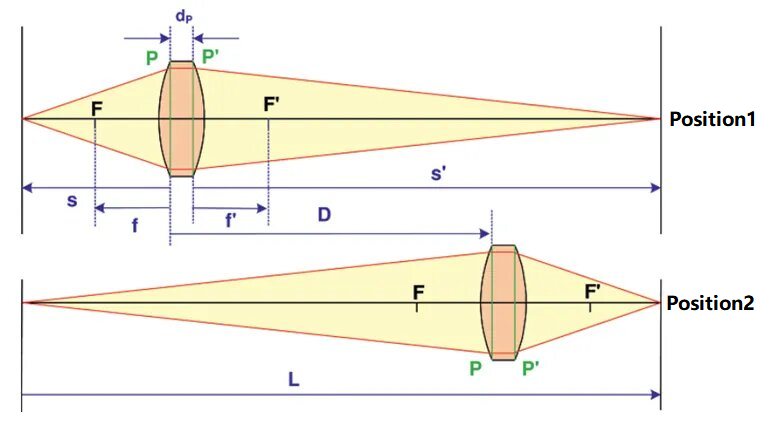
Gaussin menetelmän kaaviomainen kuva optisen järjestelmän polttovälin testaamiseksi on esitetty alla:
Kuvassa testattavan optisen järjestelmän etu- ja takapäätasoa edustavat vastaavasti P ja P', ja kahden päätason välinen etäisyys on dPTässä menetelmässä d:n arvoPpidetään tunnettuna tai sen arvo on pieni ja se voidaan jättää huomiotta. Kohde ja vastaanottonäyttö sijoitetaan vasempaan ja oikeaan päähän, ja niiden välinen etäisyys kirjataan L:nä, missä L:n on oltava suurempi kuin neljä kertaa testattavan järjestelmän polttoväli. Testattava järjestelmä voidaan sijoittaa kahteen paikkaan, jotka on merkitty vastaavasti paikoiksi 1 ja 2. Vasemmalla oleva kohde voidaan kuvata selvästi vastaanottonäytöllä. Näiden kahden paikan välinen etäisyys (merkitään D:nä) voidaan mitata. Konjugaattiyhtälön mukaan saadaan:
Näissä kahdessa kohdassa kohteiden etäisyydet tallennetaan vastaavasti s1:nä ja s2:na, jolloin s2 - s1 = D. Johtamalla kaavan voimme saada optisen järjestelmän polttovälin seuraavasti:
2.3Lensometri
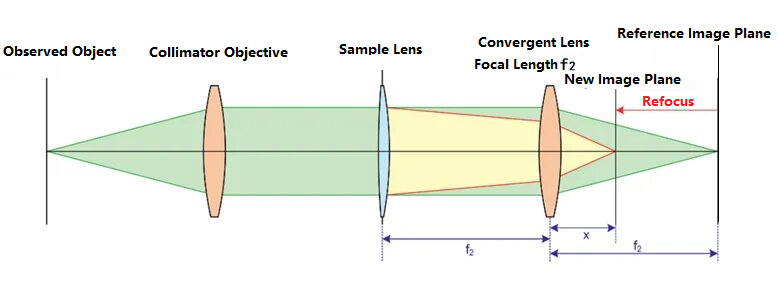
Lensometri soveltuu erittäin hyvin pitkän polttovälin optisten järjestelmien testaamiseen. Sen kaaviokuva on seuraava:
Ensinnäkin testattavaa linssiä ei sijoiteta optiselle reitille. Vasemmalla oleva havaittu kohde kulkee kollimoivan linssin läpi ja muuttuu yhdensuuntaiseksi valoksi. Yhdensuuntainen valo konvergoituu kokoavaan linssiin, jonka polttoväli on f.2ja muodostaa selkeän kuvan referenssikuvan tasossa. Kun optinen reitti on kalibroitu, testattava linssi asetetaan optiselle reitille ja testattavan linssin ja kokoavan linssin välinen etäisyys on f2Tämän seurauksena testattavan linssin toiminnan vuoksi valonsäde tarkentuu uudelleen, mikä aiheuttaa kuvatason sijainnin muutoksen ja johtaa selkeään kuvaan uuden kuvatason kohdalla kaaviossa. Uuden kuvatason ja kokoavan linssin välistä etäisyyttä merkitään x:llä. Kohde-kuvasuhteen perusteella testattavan linssin polttoväli voidaan päätellä seuraavasti:
Käytännössä linssimittaria on käytetty laajalti silmälasilinssien polttovälin mittaamiseen, ja sen etuna on yksinkertainen käyttö ja luotettava tarkkuus.
2.4 AbbeRefraktometri
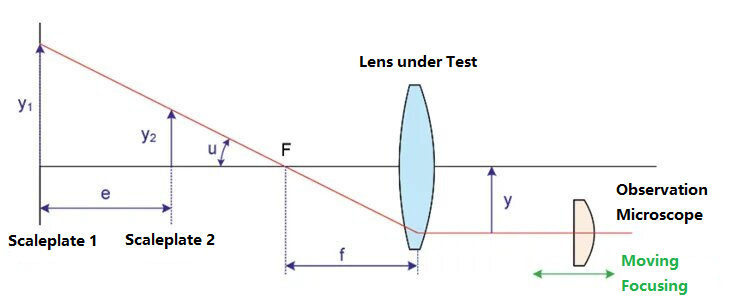
Abben refraktometri on toinen menetelmä optisten järjestelmien polttovälin testaamiseen. Sen kaaviokuva on seuraava:
Aseta testattavan linssin kohdepinnan puolelle kaksi erikorkuista viivainta, nimittäin asteikkolevyt 1 ja asteikkolevyt 2. Vastaavat asteikkolevyjen korkeudet ovat y1 ja y2. Kahden asteikkolevyn välinen etäisyys on e ja viivaimen yläviivan ja optisen akselin välinen kulma on u. Asteikkolevy kuvataan testattavalla linssillä, jonka polttoväli on f. Mikroskooppi on asennettu kuvapinnan päähän. Mikroskoopin asentoa siirtämällä löydetään kahden asteikkolevyn yläkuvat. Tällöin mikroskoopin ja optisen akselin välistä etäisyyttä merkitään y:llä. Kohde-kuvasuhteen perusteella polttoväli saadaan seuraavasti:
2.5 Moire-deflektometriaMenetelmä
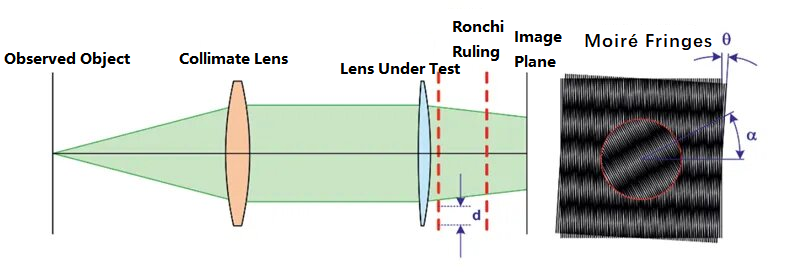
Moiré-deflektometriamenetelmässä käytetään kahta Ronchi-viivainta rinnakkaisissa valonsäteissä. Ronchi-viiva on lasialustalle kerrostettu metallikromikalvon ruudukkomainen kuvio, jota käytetään yleisesti optisten järjestelmien suorituskyvyn testaamiseen. Menetelmässä hyödynnetään kahden hilan muodostamien Moiré-juovien muutosta optisen järjestelmän polttovälin testaamiseen. Periaatteen kaavio on seuraava:
Yllä olevassa kuvassa havaittu kohde muuttuu kollimaattorin läpi kulkiessaan yhdensuuntaiseksi säteeksi. Optisella reitillä, ilman testattavan linssin lisäämistä ensin, yhdensuuntainen säde kulkee kahden hilan läpi, joiden siirtymäkulma on θ ja hilaväli d, muodostaen kuvatasoon joukon Moiré-juovia. Sitten testattava linssi asetetaan optiselle reitille. Alkuperäinen kollimoitu valo tuottaa linssin taittumisen jälkeen tietyn polttovälin. Valonsäteen kaarevuussäde voidaan laskea seuraavasta kaavasta:
Yleensä testattava linssi sijoitetaan hyvin lähelle ensimmäistä hilaa, joten yllä olevassa kaavassa R-arvo vastaa linssin polttoväliä. Tämän menetelmän etuna on, että sillä voidaan testata sekä positiivisen että negatiivisen polttovälin omaavien järjestelmien polttovälejä.
2.6 OptinenFIberAutokollimaatioMmenetelmä
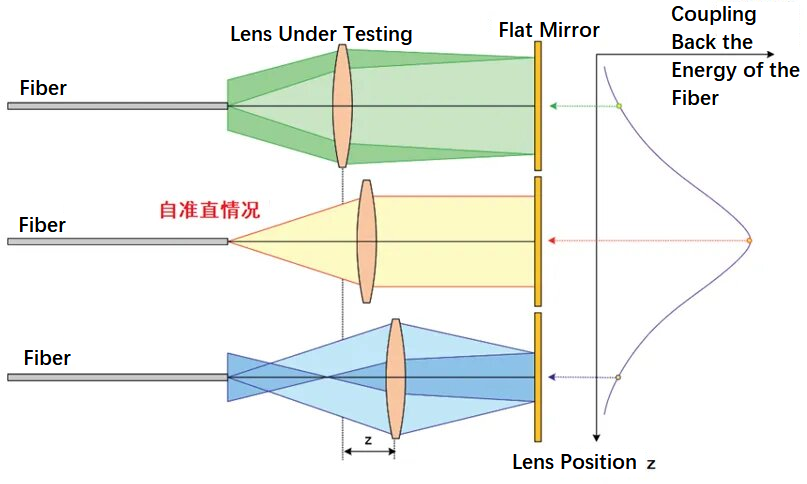
Optisen kuidun autokollimaatiomenetelmän periaate linssin polttovälin testaamisessa on esitetty alla olevassa kuvassa. Menetelmässä käytetään kuituoptiikkaa hajaantuvan säteen lähettämiseen testattavan linssin läpi ja sitten tasopeiliin. Kuvassa olevat kolme optista reittiä edustavat optisen kuidun olosuhteita polttopisteessä, polttopisteen sisällä ja polttopisteen ulkopuolella. Siirtämällä testattavan linssin asentoa edestakaisin voit löytää kuidun pään sijainnin polttopisteessä. Tällöin säde on itsekollimoitunut, ja tasopeilin heijastumisen jälkeen suurin osa energiasta palaa kuidun pään asentoon. Menetelmä on periaatteessa yksinkertainen ja helppo toteuttaa.
3. Johtopäätös
Polttoväli on tärkeä optisen järjestelmän parametri. Tässä artikkelissa käsittelemme yksityiskohtaisesti optisen järjestelmän polttovälin käsitettä ja sen testausmenetelmiä. Yhdistettynä kytkentäkaavioon selitämme polttovälin määritelmän, mukaan lukien kuvan puoleisen polttovälin, objektin puoleisen polttovälin ja edestä taakse -polttovälin käsitteet. Käytännössä on olemassa monia menetelmiä optisen järjestelmän polttovälin testaamiseen. Tässä artikkelissa esitellään kollimaattorimenetelmän, Gaussin menetelmän, polttovälin mittausmenetelmän, Abben polttovälin mittausmenetelmän, Moiré-poikkeutusmenetelmän ja optisen kuidun autokollimaatiomenetelmän testausperiaatteet. Uskon, että lukemalla tämän artikkelin saat paremman käsityksen optisten järjestelmien polttoväliparametreista.
Julkaisun aika: 09.08.2024